Question

The center of a circle is located at (3, -4). The radius of the circle is 6.

What is the equation of the circle in general form?

x2 + y2 + 6x − 8y − 11 = 0
x2 + y2 − 6x + 8y − 11 = 0
x2 + y2 + 6x − 8y + 19 = 0

Answer 1

x² + y² - 6x + 8y - 11 = 0

Explanation:

Equation of a circle:

(x - h)² + (y - k)² = r²

(x - 3)² + (y + 4)² = 6²

x² - 6x + 9 + y² + 8y + 16 = 36

x² + y² - 6x + 8y - 11 = 0

Answer 2

B

Explanation:

The equation of a circle in standard form is
`(x-h)^2+(y-k)^2=r^2`, where (h, k) is the center and r is the radius. The general form is simply the expanded form of the standard. Let's first write the standard form.

Here, the center is (3, -4) and the radius is r = 6, so:

`(x-h)^2+(y-k)^2=r^2`

`(x-3)^2+(y+4)^2=6^2`

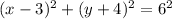
Now expand:

x² - 6x + 9 + y² + 8y + 16 = 36

x² + y² - 6x + 8y - 11 = 0

The answer is B.