Question

4) Determine the Celsius temperature of 2.49 mol of gas contained in a 2.00-L vessel at a

pressure of 143 kPa.

Answer 1

The Celsius temperature of the gas is ‪-259.34 ° C

Step-by-step explanation:

To answer the question, we note that the universal gas equation can be expressed as follows;

P·V = n·R·T

Therefore;

`T = (P \cdot V)/(R \cdot n)`

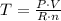
Where:

n = Number of moles = 2.49 mol

P = Pressure = 143 kPa = 143000 Pa

V = Volume = 2.00 L = ‪0.002 m³

T = Temperature in Kelvin, K = Required

R = Universal Gas Constant = 8.3145 J/(mol·K)

Plugging in the values, we have;

`T = (143000 * 0.002 )/(8.3145 * 2.49 ) = 13.81 \, K`

Hence the temperature of the gas = 13.81 K

Converting the Kelvin temperature to Celsius temperature, we have

Celsius temperature = Kelvin temperature - 273.15

Therefore, 13.81 K to Celsius temperature gives;

13.81 - 273.15 = ‪-259.34 ° C.

Answer 2

The temperature of the gas contained in the container is -259.35° C

Explanation:

To find the unit of degrees in Celsius (° C) in this case, the ideal gas law equation is used.

PV = nRT

Where P is the pressure, V is the volume, T is the temperature, n is the number of moles, and R is the universal gas constant.

• P = 143kPa = 1.4113 atm

• V = 2.00L

• n = 2.49 mol

• R = 0.08205746 atm * L / mol * K

Solving for T would be: PV / nR

T = ( 1.4113 atm * 2.00 L ) / ( 2.49 mol * 0.08205746 atm * L / mol * K )

T = 2.8226 / 0.2043

T = 13.8K = -259.35 ° C