Explaination :
So here this question is of concept linear equations. As in linear equations we assumes the unknown number as an variable after that an equation would be formed which we would solve and get the answer. Here also we would be doing same.!!
So let us assume the unknown positive integers as a and (a + 1).
★ Product of both integers :-
- a (a + 1) = 156 [Equation formed]
★ Solving the equation :-
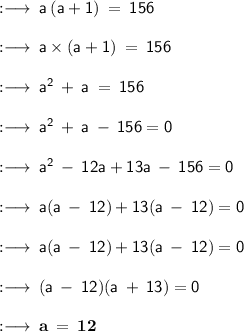
Therefore,
- First positive integer is 12
★ Second positive integer :-
- 2nd positive integer = a + 1
- 2nd positive integer = 12 + 1
- 2nd positive integer = 13