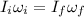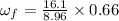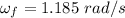Question

A student sits on a rotating stool holding two 5 kg objects. When his arms are extended horizontally, the objects are 0.9 m from the axis of rotation, and he rotates with angular speed of 0.66 rad/sec. The moment of inertia of the student plus the stool is 8 kg m2 and is assumed to be constant. The student then pulls the objects horizontally to a radius 0.31 m from the rotation axis. Calculate the final angular speed of the student.

Answer 1

Answer:
`\omega _f=1.185\ rad/s`

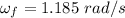
Step-by-step explanation:

Given

mass of objects
`m=5\ kg`

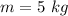
Initially mass is at
`r=0.9\ m`

Initial angular speed
`\omega_i=0.66\ rad/s`

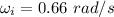
Moment of inertia of student and stool is
`I_s=8\ kg-m^2`

Finally masses are at a distance of
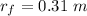`r_f=0.31\ m` from axis

`I_i=I_p+I_m`

`I_i=8+2* 5* (0.9)^2`

`I_i=16.1\ kg-m^2`

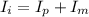
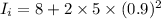
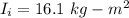
Final moment of inertia of the system

`I_f=I_s+I_m`

`I_f=8+2* 5* (0.31)^2`

`I_f=8+0.961=8.961\ kg-m^2`

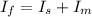
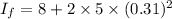
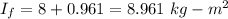
As there is no external torque therefore moment of inertia is conserved

`I_i\omega _i=I_f\omega _f`

`\omega _f=(16.1)/(8.96)* 0.66`

`\omega _f=1.796* 0.66`

`\omega _f=1.185\ rad/s`