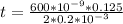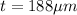Question

A wedge-shaped air film is made by placing a small slip of paper between the edges of two thin plates of glass 12.5 cm long. Light of wavelength 600 nm in air is incident normally on the glass plates. If interference fringes with a spacing of 0.200 mm are observed along the plate, how thick is the paper? This form of interferometry is a very practical way of measuring small thicknesses.

Answer 1

The thickness of the paper is
`t = 188\mu m`

Step-by-step explanation:

From the question we are told that

The length of the wedge-shaped air film
`L = 12.5 cm = (12.5)/(100) = 0.125m`

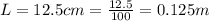
The wavelength of the light is
`\lambda = 600nm = 600* 10^(-9)m`

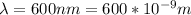
The spacing of the interference fringe is
`D = 0.200mm = (0.200)/(1000) = 0.2*10^(-3) m`

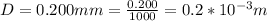
For destructive interference the thickness is mathematically represented as

`t =(\lambda * L)/(2 * D )`

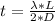
Substituting values

`t = (600 * 10^(-9) * 0.125 )/(2 * 0.2 *10^(-3))`

`t = 188\mu m`