Answer:
1, 4 or -1, -4
Explanation:
Let the two numbers be x and such that x > y.
According to the first condition:
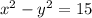
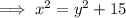 ......(1)
......(1)
According to the second condition:
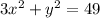
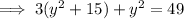
(From equation 1)
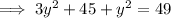
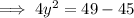
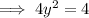
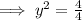
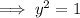
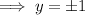
When y = 1
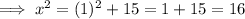
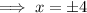
When y = -1
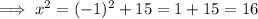
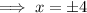
Thus, the required numbers are either 1, 4 or -1, -4