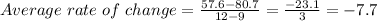Question

The average high temperature each month in a calendar year for a city in South Carolina is represented by the function: f(x)=−x2+13.3x+42

f
(
x
)
=
-
x
2
+
13
.
3
x
+
42
where x is the month. Find the average rate of change from September to December

Answer 1

`Average\hspace{3}rate\hspace{3}of\hspace{3}change=-7.7`

Explanation:

The average rate of change measures the average rate at which a function changes per unit time in a given interval. In another words, the average rate of change is the relationship between vertical and horizontal changes between two points of the function. So, basically if you are trying to find the average rate of change, you are trying to find the slope.

`Average\hspace{3}rate\hspace{3}of\hspace{3}change=Slope=m=(\Delta y)/(\Delta x) =(f(x_2)-f(x_1))/(x_2-x_1)`

If
`x` represents the months, then:

Let:

`September=x_1=9\\December=x_2=12`

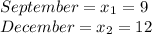
So:

For:

`f(x)=-x^2+13.3x+42`

`f(x_1)=f(9)=-(9)^2+13.3(9)+42=80.7\\\\f(x_2)=f(12)=-(12)^2+13.3(12)+42=57.6`

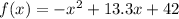
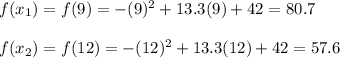
Therefore:

`Average\hspace{3}rate\hspace{3}of\hspace{3}change=(57.6-80.7)/(12-9) =(-23.1)/(3) =-7.7`