Answer:
Explanation:
Isolate the term of r, from one side of the equation.
3/2r=-1
First, multiply by 2 from both sides.
2*3/2r=2(-1)
Solve.
3r=-2
Then, you divide by 3 from both sides.
3r/3=-2/3
Solve.
Divide the numbers from left to right.
r=-2/3
-2/3=-0.66
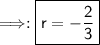
- Therefore, the correct answer is r=-2/3.
I hope this helps! Let me know if you have any questions.