Question

Does the sample provide strong evidence that the mean weight of the bags is lower than the 35.6 grams listed on the package? Group of answer choices Yes, because a random sample of 100 bags with a mean weight below 33.6 grams is very unlikely if the individual bags have a mean weight of 35.6 grams. No, because random samples of 100 bags will have mean weights that vary. A mean weight around 33.6 grams is not unusual. No, because the mean weight of the sample is only off by 2 grams. Yes, because 33.6 is less than 35.6 grams

Answer 1

As probability of that happening is very small; Yes, 33.6 is less than 35.6 grams because it provide strong evidence that the mean weight of the bags is lower than the 35.6 grams listed on the package.

Explanation:

For a normal distribution Z-score

`Z = (X-\mu)/(\sigma)`

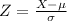
Given that :

the mean (
`\mu`) = 35.6

standard deviation (
`\sigma`) = 5.2

sample size (n) = 35

standard error:
`\sigma_x = (\sigma)/(√(n))`

`\sigma_x = (5.2)/(√(35))`

`\sigma_x = 0.879`

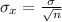
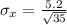
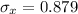
The probability that a random sample of 35 bags has a mean weight of 33.6 grams or less is :

P(X<33.6) = P(Z < - 2.28)

= 0.0114

Conclusion:

As probability of the happening is very small; Yes, 33.6 is less than 35.6 grams because it provide strong evidence that the mean weight of the bags is lower than the 35.6 grams listed on the package.