Answer:
![\vec{v_R}=\hat{i}[-329.11]+\hat{j}[516.18]](https://img.qammunity.org/2021/formulas/physics/college/lq2ipqz0go4hey4tizz2e78jmzcjtme2y9.png)
Step-by-step explanation:
Given
Plane is initially flying with velocity of magnitude
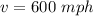
at angle of
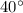 with North towards west
with North towards west
Velocity of plane airplane can be written as
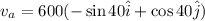
Now wind is encountered with speed of
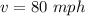 at angle of
at angle of
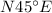
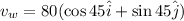
resultant velocity
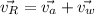
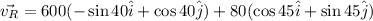
![\vec{v_R}=\hat{i}[-385.67+56.56]+\hat{j}[459.62+56.56]](https://img.qammunity.org/2021/formulas/physics/college/h3m07qng4sgqtpy7cpea3eh7g7m94x3wmy.png)
![\vec{v_R}=\hat{i}[-329.11]+\hat{j}[516.18]](https://img.qammunity.org/2021/formulas/physics/college/lq2ipqz0go4hey4tizz2e78jmzcjtme2y9.png)
for direction

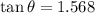
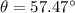 west of North
west of North