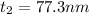Question

Laser light of wavelength 510 nm is traveling in air andshines at normal incidence onto the flat end of a transparent plasticrod that has n = 1.30. The end of the rod has a thin coating ofa transparent material that has refractive index 1.65. Whatis theminimum (nonzero) thickness of the coating (a) for which thereis maximum transmission of the light into the rod; (b) for whichtransmission into the rod is minimized?

Answer 1

a

The thickness is
`t_1 = 155nm`

b

The thickness is
`t_2 =77.3 nm`

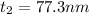
Step-by-step explanation:

From the question we are told that

The wavelength of the laser light is
`\lambda = 510 nm = 510*10^(-9) m`

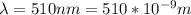
The refractive index of the plastic rod is
`n = 1.30`

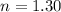
The refractive index of the transparent coating is
`n__(T)} = 1.65`

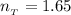
For maximum transmission of light into the rod the reflection would be minimum and this minimum reflection is mathematically represented as

`2 t_1 = m (\lambda )/(n___(T))}`

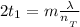
Where m is the order of interference which is equal to 1

t is the thickness

Substituting values

`2 t_1 = (510*10^(-9))/(1.65)`

`t_1 = (510*10^(-9))/( 2 * 1.65)`

`t_1 = 155nm`

For minimum transmission of light into the rod the reflection would be maximum and this maximum reflection is mathematically represented as

`2t_2 = [ m + (1)/(2) ] (\lambda )/(n__(T))}`

Where m = 0 this because the transmission of light is minimum

Substituting values

`2t_2 = [ 0 + (1)/(2) ] (510 *10^(-9) )/(1.65)`

`t_2 = [ 0 + (1)/(2) ] (510 *10^(-9) )/( 2 * 1.65)`

`t_2 =77.3 nm`