Question

Given: EL- tangent, EK- secant
Prove: EJ·LK = EL·LJ

Answer 1

This is possible.

Explanation:

We can say that m<E=m<E, because of the Reflexive Property

Then, we have angles JKL and ELJ, which are equal through the peripheral angle theorem.

With these two angles, we can say that triangles ELK and EJL are similar, by the Angle-Angle Postulate (AA).

Then we can create this ratio through the Corresponding Parts of Similar Triangles Theorem, (CPST),
`(LK)/(LJ) =(EL)/(EJ)`.

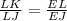With this ratio, we can cross multiply to get the desired result

`EJ`·
`LK=EL`·
`LJ`

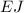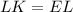Hope this helps with your RSM problem

Yup, i caught ya.