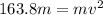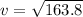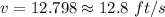Question

A hula hoop is rolling along the ground with a translational speed of 26 ft/s. It rolls up a hill that is 16 ft high. Determine whether the hoop makes it to the top\of the hill. If the hoop makes it to the top, what is its translational speed at the top? If the hoop does not make it to the top, how far vertically up does it rise before stopping? (Hint: A hula hoop is a uniform ring. Apply energy conservation for a rolling object.)

Answer 1

Answer:12.8 ft/s

Step-by-step explanation:

Given

Speed of hoop
`v=26\ ft/s`

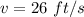
height of top
`h=16\ ft`

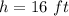
Initial energy at bottom is

`E_b=(1)/(2)mv^2+(1)/(2)I\omega ^2`

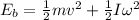
Where m=mass of hoop

I=moment of inertia of hoop

`\omega`=angular velocity

for pure rolling
`v=\omega R`

`I=mR^2`

`E_b=(1)/(2)mv^2+(1)/(2)mR^2* ((v)/(R))^2`

`E_b=mv^2=m(26)^2=676m`

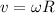
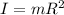
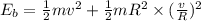
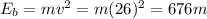
Energy required to reach at top

`E_T=mgh=m* 32.2* 16`

`E_T=512.2m`

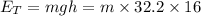
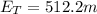
Thus 512.2 m is converted energy is spent to raise the potential energy of hoop and remaining is in the form of kinetic and rotational energy

`\Delta E=676m-512.2m=163.8m`

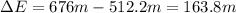
Therefore

`163.8 m=mv^2`

`v=√(163.8)`

`v=12.798\approx 12.8\ ft/s`