Question

Nicolas has $6,500 to deposit into an account which earns 3.25% interest compounded annually. How interest will he have earned at the end of 8 years.

Answer 1

We have been given that Nicolas has $6,500 to deposit into an account which earns 3.25% interest compounded annually. We are asked to find amount of interest earned at the end on 8 years.

We will use compound interest formula to solve our given problem.

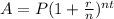`A=P(1+(r)/(n))^(nt)`, where,

A = Final amount,

P = Principal amount,

r = Annual interest rate in decimal form,

n = Number of times interest is compounded per year,

t = Time in years.

`3.25\%=(3.25)/(100)=0.0325`

`A=6500(1+(0.0325)/(1))^(1\cdot 8)`

`A=6500(1+0.0325)^(8)`

`A=6500(1.0325)^(8)`

`A=6500(1.2915775352963673)`

`A=8395.253979`

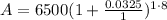
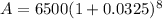
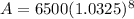
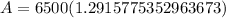
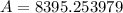
Now we will subtract principal amount from final amount to find amount of interest as:

`\text{interest}=8395.253979-6500`

`\text{interest}=1895.253979\approx 1895.25`

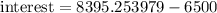
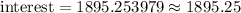
Therefore, Nicolas would have earned $1895.25 in interest at the end of 8 years.