Question

Graph this parabola
Show all steps please!!!

Answer 1

Vertex

Vertex form of a quadratic equation:

`y=a(x-h)^2+k\quad \textsf{where }(h,k)\:\textsf{is the vertex}`

Given equation:
`y=3(x+2)^2-1`

Therefore, the vertex is (-2, -1)

x-intercepts (zeros)

The x-intercepts are when
`y=0`:

`\implies 3(x+2)^2-1=0`

`\implies 3(x+2)^2=1`

`\implies (x+2)^2=\frac13`

`\implies x+2=\pm√(\frac13)`

`\implies x+2=\pm(√(3))/(3)`

`\implies x=-2\pm(√(3))/(3)`

`\implies x=(-6\pm√(3))/(3)`

Therefore, the x-intercepts are at -2.6 and -1.4 (nearest tenth)

y-intercept

The y-intercept is when
`x=0`:

`\implies 3(0+2)^2-1=11`

So the y-intercept is at (0, 11)

Plot the graph

• As the leading coefficient is positive, the parabola will open upwards.
• Plot the vertex at (-2, -1)
• Plot the x-intercepts (-2.6, 0) and (-1.4, 0)
• Plot the y-intercept (0, 11)

The axis of symmetry is the x-value of the vertex. Therefore, the parabola is symmetrical about x = -2

**You don't need to plot the axis of symmetry - I have added it so that it is easier to draw the curve**

Answer 2

In this case, the equation is in vertex form. To graph the parabola, we need to determine the y-intercept, x-intercept(s), and the vertex.

Vertex of Parabola:

Vertex form: y = a(x + h)² - k

• ⇒ [y = 3(x + 2)² - 1] and [y = a(x - h)² - k]
• ⇒ Vertex: (h, k) ⇒ (-2, -1)

X-intercept(s) of Parabola:

Assume "y" as 0.

`\implies 0 = 3(x + 2)^(2) - 1`

`\implies 1 = 3(x + 2)^(2)`

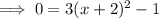
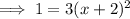
Take square root both sides and simplify:

`\implies√(1) = \sqrt{3(x + 2)^(2)}`

`\implies1 = √(3 * (x + 2) * (x + 2))`

`\implies1 = (x + 2) * \sqrt{3`

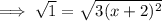
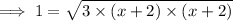
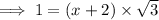
Divide √3 both sides:

`\implies \±\huge\text{(}(1 )/(√(3)) \huge\text{)} = (x + 2)`

`\implies \±\huge\text{(}(√(1) )/(√(3)) \huge\text{)} = (x + 2)`

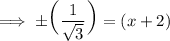
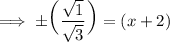
Multiply √3 to the numerator and the denominator:

`\implies \±\huge\text{(}\frac{√(1) * √(3) }{\sqrt{3* √(3)}} \huge\text{)} = (x + 2)`

`\implies \±\huge\text{(}(√(3) )/(3)} \huge\text{)} = (x + 2)`

`\implies \±\huge\text{(}(√(3) )/(3)} \huge\text{)} - 2 =x`

`\implies x = \underline{-2.6...} \ \text{and} \ \underline{-1.4...} \ \ \ \ (\text{Nearest tenth})`

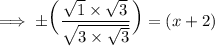
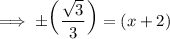
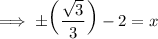
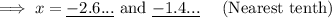
Y-intercept of Parabola:

Assume "x" as 0.

• ⇒ y = 3(0 + 2)² - 1
• ⇒ y = 3(2)² - 1
• ⇒ y = 3(4) - 1
• ⇒ y = 12 - 1
• ⇒ y = 11

y-intercept = 11 ⇒ (0, 11)

Determining the direction of the parabola:

Since the first cooeficient is positive (+3), the direction of the parabola will be upwards.

Determining the axis of symmetry line:

Axis of symmetry line: x-coordinate of vertex

Axis of symmetry line: x = -2

Plot the following on the graph:

• y-intercept ---> 11 -----> (0, 11)
• x-intercept(s) -----> -1.4 and -2.6 -------> (-1.4, 0) and (-2.6, 0)
• Vertex -------> (-2, -1)
• Axis of symmetry ----> x = -2

Refer to graph attached.