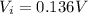Answer:
The maximum voltage across the inductor is
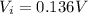
Step-by-step explanation:
From the question we are told that
The amplitude of the power is
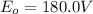
The resistance is
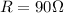
The capacitance is
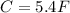
The inductance is
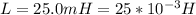
According to the question the the circuit frequency is resonance frequency
At resonance frequency
capacitive Reactance is equal to the Inductive Reactance
The capacitive Reactance is mathematically represented as
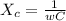
Where
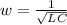
Substituting values
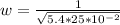
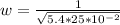
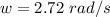
So
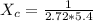
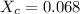
The inductive Reactance is mathematically represented as
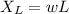
Substituting values
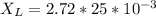
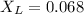
The impedance of the circuit is mathematically represented as
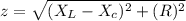
Substituting values

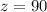
The maximum current supplied to the circuit is

So
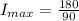
=>

Now the maximum voltage across the inductor is
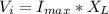
So
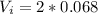
=>