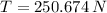Answer:
Step-by-step explanation:
The vine experiments a centripetal acceleration while swinging (the stuntsman experiments a centrifugal acceleration), whose most critical point occurs at the bottom and can be described by the Newton's Laws:

The minimum tension force that the vine must be able to support without breaking is:
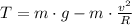
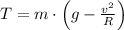
![T = (82\,kg)\cdot \left[9.807\,(m)/(s^(2))-(\left(9\,(m)/(s) \right)^(2))/(12\,m) \right]](https://img.qammunity.org/2021/formulas/physics/college/uuca9zwt554ehnolefzj93e88h53f4j1jt.png)