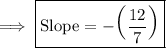Question

What is the slope of the line that passes
* through the points (8, -9) and (1, 3)?

Answer 1

`\boxed{\text{Slope} = -\huge\text{(}(12)/(7)\huge\text{)}}`

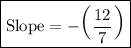
Explanation:

Slope formula:

`\text{Slope} = \frac{\text{Rise}}{\text{Run}}} = (y_(2) - y_(1))/(x_(2) - x_(1))`

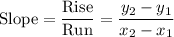
Using the coordinates (8, -9) and (1, 3), we obtain the following:

• First point = (x₁, y₁) = (8, 9) = x₁ = 8 y₁ = 9

• Second point = (x₂, y₂) = (1, 3) = x₂ = 1 y₂ = 3

Substitute the coordinates of both the points in the slope formula to obtain the fraction that represents the slope.

`\implies \text{Slope} = (3 - (- 9))/(1 - 8)`

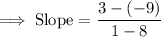
To obtain a specific fraction or whole number that represents the slope, we need to simplify the numerator and the denominator.

`\implies \text{Slope} = (3 + 9)/(-7)`

`\implies \text{Slope} = (12)/(-7)`

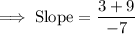
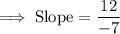
Use parenthesis and take out the "negative sign" from the denominator.

`\implies \boxed{\text{Slope} = -\huge\text{(}(12)/(7)\huge\text{)}}`

Answer 2

• 
  `\boxed{\sf{-(12)/(7) }}`

Explanation:

Use the slope formula.

`\underline{\text{SLOPE FORMULA:}}`

`\longrightarrow: \sf{(y_2-y_1)/(x_2-x_1) }`

y2=3

y1=(-9)

x2=1

x1=8

Rewrite the problem down.

`\sf{(3-(-9))/(1-8)=(3+9)/(1-8)=(12)/(-7)=\boxed{\sf{-(12)/(7) }}`

• Therefore, the slope is -12/7.

I hope this helps, let me know if you have any questions.