Question

A random sample of 77 fields of corn has a mean yield of 26.226.2 bushels per acre and standard deviation of 2.322.32 bushels per acre. Determine the 95%95% confidence interval for the true mean yield. Assume the population is approximately normal. Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.

Answer 1

Therefore the 95% confidence interval is (25,707.480 < E < 26,744.920)

Explanation:

n = 77

mean u = 26,226.2 bushels per acre

standard deviation s = 2,322.32

let E = true mean

let A = test statistic

Find 95% Confidence Interval

so

let A = (u - E) * (
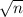`√(n)` / s) be the test statistic

we want P( average_l < A < average_u ) = 95%

look for lower 2.5% and the upper 97.5% Because I think this is a 2-tail test

average_l = -1.96 which corresponds to the 2.5%

average_u = 1.96

P( -1.96 < A < 1.96) = 95%

P( -1.96 < (u - E) * (
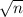`√(n)` / s) < 1.96) = 95%

Solve for the true mean E ok

E < u + 1.96* (s /
`√(n)`)

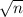from -1.96 < (u - E) * (
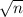`√(n)` / s)

E < 26,226.2 + 1.96*( 2,322.32 /
`√(77)` )

E < 26,226.2 + 1.96*( 2,322.32 /
`√(77)` )

E < 26,226.2 + 518.7197348105429466

upper bound is 26,744.9197

or

u - 1.96* (s /
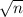`√(n)`) < E

26,226.2 - 518.7197348105429466 < E

25,707.48026519 < E

lower bound is 25,707.48026519

Therefore the 95% confidence interval is (25,707.480 < E < 26,744.920)