Question

Leroy shoots a basketball through the air in an attempt to score two points.

The height h of the ball in feet as a function of the distance d in feet that the

ball travels horizontally is given by h = −d^2 + 10d + 5. How far horizontally

from Leroy will the ball land on the ground if it does not hit the backboard or

the rim of the basket?

Answer 1

10.47 feet.

Explanation:

The height, h of Leroy's ball is given by the function:

`h = -d^2 + 10d + 5.`

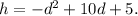
If the ball does not hit the backboard or the rim of the basket but lands on the ground, then at that point, its height h(d)=0

Therefore:

`h = -d^2 + 10d + 5=0`

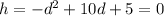
We solve the above for the values of d.

`-d^2 + 10d + 5=0`

a=-1, b=10, c=5

Using quadratic formula:

`d=(-b\pm√(b^2-4ac) )/(2a) \\=(-10\pm√(10^2-4*-1*5) )/(2*-1) \\=(-10\pm√(120) )/(-2) \\d=(-10 + √(120) )/(-2)=-0.4772\\OR:\\d=(-10 - √(120) )/(-2)=10.4772`

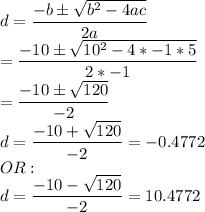
Therefore, the horizontal distance of the ball from Leroy is 10.47 feet.