Answer:
Explanation:
Since this question is lacking the matrix A, we will solve the question with the matrix
![\left[\begin{matrix}4 & -2 \\ 1 & 1 \end{matrix}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/hpi21zvghbfncekt0nmyeug2zkcbkrpovc.png)
so we can illustrate how to solve the problem step by step.
a) The characteristic polynomial is defined by the equation
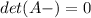 where I is the identity matrix of appropiate size and lambda is a variable to be solved. In our case,
where I is the identity matrix of appropiate size and lambda is a variable to be solved. In our case,
![\left|\left[\begin{matrix}4-\lamda & -2 \\ 1 & 1-\lambda \end{matrix}\right]\right|= 0 = (4-\lambda)(1-\lambda)+2 = \lambda^2-5\lambda+4+2 = \lambda^2-5\lambda+6](https://img.qammunity.org/2021/formulas/mathematics/college/utcn45yoegays8b8yn8jsunshsohqnwecd.png)
So the characteristic polynomial is
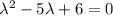 .
.
b) The eigenvalues of the matrix are the roots of the characteristic polynomial. Note that
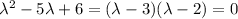
So
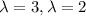
c) To find the bases of each eigenspace, we replace the value of lambda and solve the homogeneus system(equalized to zero) of the resultant matrix. We will illustrate the process with one eigen value and the other one is left as an exercise.
If
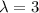 we get the following matrix
we get the following matrix
![\left[\begin{matrix}1 & -2 \\ 1 & -2 \end{matrix}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/1dtgudkm541d6mod5fisr273ny2r2aasch.png) .
.
Since both rows are equal, we have the equation
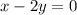 . Thus x=2y. In this case, we get to choose y freely, so let's take y=1. Then x=2. So, the eigenvector that is a base for the eigenspace associated to the eigenvalue 3 is the vector (2,1)
. Thus x=2y. In this case, we get to choose y freely, so let's take y=1. Then x=2. So, the eigenvector that is a base for the eigenspace associated to the eigenvalue 3 is the vector (2,1)
For the case
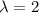 , using the same process, we get the vector (1,1).
, using the same process, we get the vector (1,1).
d) By definition, to diagonalize a matrix A is to find a diagonal matrix D and a matrix P such that
 . We can construct matrix D and P by choosing the eigenvalues as the diagonal of matrix D. So, if we pick the eigen value 3 in the first column of D, we must put the correspondent eigenvector (2,1) in the first column of P. In this case, the matrices that we get are
. We can construct matrix D and P by choosing the eigenvalues as the diagonal of matrix D. So, if we pick the eigen value 3 in the first column of D, we must put the correspondent eigenvector (2,1) in the first column of P. In this case, the matrices that we get are
![P=\left[\begin{matrix}2&1 \\ 1 & 1 \end{matrix}\right], D=\left[\begin{matrix}3&0 \\ 0 & 2 \end{matrix}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/h0gdkvhimlyppqwg0zhkk4q0rzzqwmrpd6.png)
This matrices are not unique, since they depend on the order in which we arrange the eigenvalues in the matrix D. Another pair or matrices that diagonalize A is
![P=\left[\begin{matrix}1&2 \\ 1 & 1 \end{matrix}\right], D=\left[\begin{matrix}2&0 \\ 0 & 3 \end{matrix}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/9c05hrs2v7620zdvtp7gtjucntaciggqbo.png)
which is obtained by interchanging the eigenvalues on the diagonal and their respective eigenvectors