Question

Does a statistics course improve a student's mathematics skills,as measured by a national test? Suppose a random sample of 13 students takes the same national mathematics exam prior to enrolling in a stats course and just after completing the course. At a 1% level of significance determine whether the scores after the stats course are significantly higher than the scores before. Take the differences = before - after.

Answer 1

There is not enough evidence to support the claim that the scores after the stats course are significantly higher than the scores before (the difference in the scores is higher than 0).

P-value=0.042.

Explanation:

The question is incomplete:

The data of the scores for each student is:

Before After

430 465

485 475

520 535

360 410

440 425

500 505

425 450

470 480

515 520

430 430

450 460

495 500

540 530

We will generate a sample for the difference of scores (before - after) and test that sample.

The sample of the difference is [35 -10 15 50 -15 5 25 10 5 0 10 5 -10]

This sample, of size n=13, has a mean of 9.615 and a standard deviation of 18.423.

The claim is that the scores after the stats course are significantly higher than the scores before (the difference in the scores is higher than 0).

Then, the null and alternative hypothesis are:

`H_0: \mu=0\\\\H_a:\mu> 0`

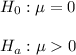
The significance level is 0.01.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(18.423)/(√(13))=5.11`

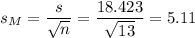
Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(9.615-0)/(5.11)=(9.615)/(5.11)=1.882`

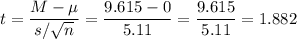
The degrees of freedom for this sample size are:

`df=n-1=13-1=12`

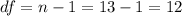
This test is a right-tailed test, with 12 degrees of freedom and t=1.882, so the P-value for this test is calculated as (using a t-table):

`P-value=P(t>1.882)=0.042`

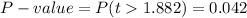
As the P-value (0.042) is bigger than the significance level (0.01), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the scores after the stats course are significantly higher than the scores before (the difference in the scores is higher than 0).