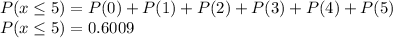Answer:
25. P(6) = 0.1721
26. P(9) = 0.0294
27.
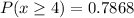
28.
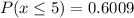
Explanation:
When we have n identical and independent events with a probability p of success and (1-p) of fail, we have a Binomial distribution. So, the probability that x events are success is calculated as:

So, the probability that x families hardly ever pay off the balance follows a binomial distribution and it is calculated as:
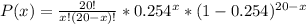
where n is 20 and p is 0.254.
Then, the probability that exactly 6 families hardly ever pay off the balance is:
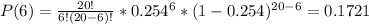
The probability that exactly 9 families hardly ever pay off the balance is:
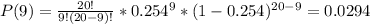
The probability that at least 4 families hardly ever pay off the balance is:
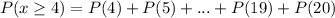
So, using the same equation to find every probability, we get:
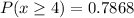
Finally, the probability that at most 5 families hardly ever pay off the balance is: