Answer:
The restocking level should be 50 cuffs.
Explanation:
Let X = restocking level of blood pressure cuff repair parts.
The mean number of adult arm cuffs used is, μ = 40.
And the standard deviation is, σ = 6.
It is provided that manager would like to avoid the embarrassment of a stock-out at least 95% of the time.
Assume that the random variable X follows a Normal distribution.
Then, from the provided data is can be said that:
P (X < x) = 0.95
⇒ P (Z < z) = 0.95
The value of z for the above probability is:
z = 1.65.
Compute the value of X as follows:
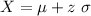

Thus, the restocking level should be 50 cuffs.