Question

Grandma and grandpa are painting gutters of their house. Grand leans a 12 foot ladder against the house which reaches 9 ft up the side of the house. How far away from the house is the base of the ladder? Please help my last

Answer 1

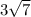`3√(7)` feet away from the house.

Explanation:

This problem may seem a bit confusing, but after analyzing it closely we can see that Grand leaning on a ladder against the house forms a triangle, in which they want to know one of the legs.

Assuming that it is a right triangle, we can apply the Pythagorean Theorem:

`L^(2) + L^(2) = H^(2)`

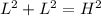
Since the ladder is leaning against the house, and the houses side is our right angle, the ladder's height is our hypotenuse.

Therefore, we must reverse, or do the inverse of our formula:

`H^(2) - L^(2) = L^(2)`

`12^(2) - 9^(2) = 144 - 81\\144 - 81 = 63\\l^(2) = 63\\\`

`l = √(63)`

`√(63) = 3√(7).`

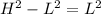
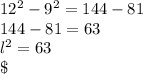
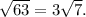
Thusly, the base is
`\boxed{3√(7){\text{\:feet\:away\:from\:the\:house.}}}`

Hope this helps! ((: