Question

A philosophy professor assigns letter grades on a test according to the following scheme. A: Top 14% of scores B: Scores below the top 14% and above the bottom 60% C: Scores below the top 40% and above the bottom 18% D: Scores below the top 82% and above the bottom 8% F: Bottom 8% of scores Scores on the test are normally distributed with a mean of 76.9 and a standard deviation of 7.4. Find the minimum score required for an A grade. Round your answer to the nearest whole number, if necessary.

Answer 1

The minimum score required for an A grade is 85.

Explanation:

The grade distribution on a test is:

Grade Criteria

A Top 14%

B < Top 14% - > Bottom 60%

C < Top 40% - > Bottom 18%

D < Top 82% - > Bottom 8%

F Bottom 8%

Le the random variable X denote the scores on the test.

The random variable X is normally distributed with parameters μ = 76.9 and standard deviation, σ = 7.4.

To compute the probability of a normally distributed random variable we first need to convert the raw scores to the z-scores.

`z=(x-\mu)/(\sigma)`

The distribution of these z-scores are known as the standard normal distribution, i.e. Z follows N (0, 1).

Now it is provided that a student has to score in the top 14% to receive a grade A.

That is, P (X > x) = 0.14.

⇒ P (X < x) = 1 - 0.14

= 0.86

⇒ P (Z < z) = 0.86

The value of z for this probability is:

z = 1.08.

*Use a z-table for the probability.

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)`

`x=\mu + z\ \sigma`

`=76.9+(1.08* 7.4)\\=76.9+7.992\\=84.892\\\approx 85`

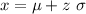
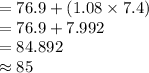
Thus, the minimum score required for an A grade is 85.