Question

A circle is centered at N(-6, -2). The point E(-1,1) is on the circle.

Where does the point H(-10, – 7) lie?
Choose 1 answer:

Inside the circle

On the circle

Outside the circle

Answer 1

Outside the circle

Explanation:

Radius: NE

sqrt[(-10--6)² + (-7--2)²]

sqrt(34)

Distance NH

sqrt[(-1--6)² + (1--2)²]

sqrt(41)

Distance NH > radius,

So outside the circle

Answer 2

Outside the circle

Explanation:

Let's first write the equation of this circle:
`(x-h)^2+(y-k)^2=r^2`, where (h, k) is the center and r is the radius. Here, the center is (-6, -2). We need to find the radius, which will just be the distance from N to E:

NE =
`√((-6-(-1))^2+(-2-1)^2) =√(25+9) =√(34)`

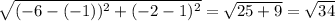
The radius is √34, which means that r² = 34. So, our equation is:

(x + 6)² + (y + 2)² = 34

Plug in -10 for x and -7 for y:

(x + 6)² + (y + 2)² = 34

x² + 12x + 36 + y² + 4y + 4 = 34

x² + 12x + y² + 4y + 40 = 34

x² + 12x + y² + 4y + 6 = 0

(-10)² + 12 * (-10) + (-7)² + 4 * (-7) + 6 = 7

Since 7 > 0, we know that H lies outside the circle.