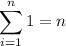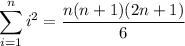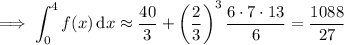Question

Estimate the area underneath the curve by evaluating the Rieman sum using 6 rectangles

Answer 1

Split up the interval [0, 4] into 6 subintervals of equal length (4-0)/6 = 2/3:

[0, 2/3], [2/3, 4/3], [4/3, 2], [2, 8/3], [8/3, 10/3], [10/3, 4]

The right endpoints form an arithmetic sequence,

`r_i=\frac23+\frac{2(i-1)}3=\frac{2i}3`

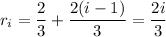
where
`i=1,2,3,\ldots,6`.

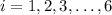We estimate the area under the curve over each subinterval by a rectangle with length 2/3 and height equal to the value of the function at the right endpoint. Then the value of the integral is approximately equal to the sum of these rectangles' areas:

`\displaystyle\int_0^4f(x)\,\mathrm dx\approx\frac23\sum_(i=1)^6f(r_i)`

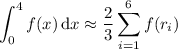
We have
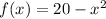`f(x)=20-x^2`, so

`f(r_i)=f\left(\frac{2i}3\right)=20-\frac{4i^2}9`

`\implies\displaystyle\int_0^4f(x)\,\mathrm dx\approx\frac{40}3\sum_(i=1)^61+\left(\frac23\right)^3\sum_(i=1)^6i^2`

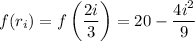
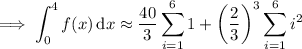
Recall that

`\displaystyle\sum_(i=1)^n1=n`

`\displaystyle\sum_(i=1)^ni^2=\frac{n(n+1)(2n+1)}6`

`\implies\displaystyle\int_0^4f(x)\,\mathrm dx\approx\frac{40}3+\left(\frac23\right)^3\frac{6\cdot7\cdot13}6=(1088)/(27)`