Question

A right triangle has side lengths a, b, and c as shown below.

Use these lengths to find cosx, sinx, and tanx.
COSX =
[]
DO X
sinx =
tan x =

Answer 1

`\bold{\sin x = (b)/(c)}\bold{\\\cos x = (a)/(c)}\bold{\\\tan x = (b)/(a)}`

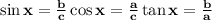
Explanation:

Given that

A right triangle has side lengths a, b, and c

Because you did not attached photo of the right triangle so I will assume that:

• Side a is the adjacent (A)
• Side b is the opposite (O)
• Side c is the hypotenuse (H)

(Please have a look at the attached photo)

To solve for the trigonometric functions of x, we need to recall the ratios they represent as shown below.

`\sin x = (O)/(H)\\\cos x = (A)/(H)\\\tan x = (O)/(A)`

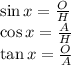
EX: the sine of x is equal to the side opposite of angle x over the hypotenuse. Hence, we have the expressions of the trigonometric functions as shown below:

`\bold{\sin x = (b)/(c)}\bold{\\\cos x = (a)/(c)}\bold{\\\tan x = (b)/(a)}`

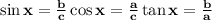
Hope it will find you well