Answer:
67 and 70
Explanation:
Mean grade (μ) = 79.7
Standard deviation (σ) = 9.7
D: Scores below the top 83% and above the bottom 9%, which means scores between the 9th and 17th percentile.
z-score at the 9th percentile: -1.34
z-score at the 17th percentile: -0.955
The lower limit of a D grade is:
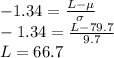
The upper limit of a D grade is:

Rounding to the nearest whole number, the limits for a D grade are 67 and 70.