Answer:
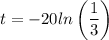
Explanation:
The relationship between A, the area of the glacier in square kilometers, and t, the number of years the glacier has been melting, is modeled by the equation.:
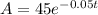
We want to determine the value of t for which the area, A(t)=15 square kilometers.
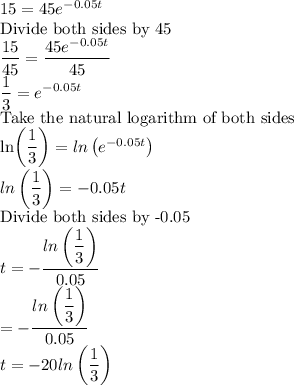
Therefore, the time for which the area will be 15 sqyare kilometers is:
-20 ln(1/3) years.