Answer:
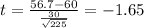
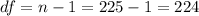
The p value would be:
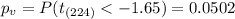
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we cna conclude that the true mean is less than 60 at 10% of significance.
Explanation:
Information given
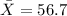 represent the sample mean of interest
represent the sample mean of interest
 represent the sample standard deviation
represent the sample standard deviation
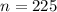 sample size
sample size
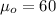 represent the value to check
represent the value to check
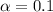 represent the significance level for the hypothesis test.
represent the significance level for the hypothesis test.
t would represent the statistic (variable of interest)
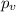 represent the p value for the test
represent the p value for the test
System of hypothesis
we want to check if the true mean is lower than 60, so thn the system of hypothesis are:
Null hypothesis:
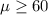
Alternative hypothesis:
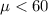
The statistic is given by:
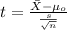 (1)
(1)
Replcing into the formula we got:
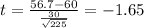
P value
The degrees of freedom are given by:
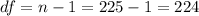
The p value would be:
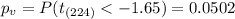
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true mean is less than 60 at 10% of significance.