Answer:
The minimum sample size required to ensure that the estimate has an error of at most 0.14 at the 95% level of confidence is n=567.
Explanation:
We have to calculate the minimum sample size n needed to have a margin of error below 0.14.
The critical value of z for a 95% confidence interval is z=1.96.
To do that, we use the margin of error formula in function of n:
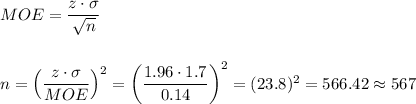
The minimum sample size to have this margin of error is n = 567.