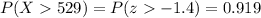Question

Farmers often sell tomatoes at roadside stands during the summer. One such roadside stand has a daily demand for tomatoes that is normally distributed with a mean equal to 571 tomatoes per day and a standard deviation equal to 30 tomatoes per day. If there are 529 tomatoes available to be sold at the roadside stand at the beginning of a day, what is the probability that they will all be sold?

Answer 1

The probability that the 529 tomatoes will all be sold is P=0.919.

Explanation:

We have the variable X: sold tomatoes, modeled by a normal distribution with mean 571 and standard deviation 30.

The probability of selling 529 tomatoes is mathematically equal to the probability of selling 529 tomatoes or more (at least 529 tomatoes).

To calculate this probability, we first calculate the z-score for X=529.

`z=(X-\mu)/(\sigma)=(529-571)/(30)=(-42)/(30)=-1.4`

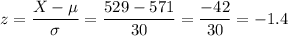
The probability of selling the 529 tomatoes is then:

`P(X>529)=P(z>-1.4)=0.919`