Answer:
The least number of tennis balls needed for the sample is 1849.
Explanation:
The (1 - α) % confidence interval for population proportion is:
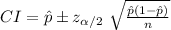
The margin of error for this interval is:
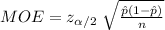
Assume that the proportion of all defective tennis balls is p = 0.50.
The information provided is:
MOE = 0.03
Confidence level = 99%
α = 1%
Compute the critical value of z for α = 1% as follows:
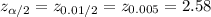
*Use a z-table.
Compute the sample size required as follows:
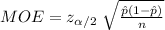
![n=[(z_(\alpha/2)* √(\hat p(1-\hat p)) )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/u8xrlsot42hymhv1r8tf3bn36vnxzmeeby.png)
![=[(2.58* √(0.50(1-0.50)) )/(0.03)]^(2)\\\\=1849](https://img.qammunity.org/2021/formulas/mathematics/college/c44gsrufx1651c8hxo6hs4w6sidpaol2p7.png)
Thus, the least number of tennis balls needed for the sample is 1849.