Answer:
(a) 95% confidence interval for the true average porosity of a certain seam is [4.52 , 5.18].
(b) 98% confidence interval for the true average porosity of a another seam is [4.12 , 4.99].
Explanation:
We are given that the helium porosity (in percentage) of coal samples taken from any particular seam is normally distributed with true standard deviation 0.75.
(a) Also, the average porosity for 20 specimens from the seam was 4.85.
Firstly, the pivotal quantity for 95% confidence interval for the population mean is given by;
P.Q. =
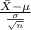 ~ N(0,1)
~ N(0,1)
where,
 = sample average porosity = 4.85
= sample average porosity = 4.85
 = population standard deviation = 0.75
= population standard deviation = 0.75
n = sample of specimens = 20
 = true average porosity
= true average porosity
Here for constructing 95% confidence interval we have used One-sample z test statistics as we know about population standard deviation.
So, 95% confidence interval for the true mean,
 is ;
is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
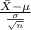 < 1.96) = 0.95
< 1.96) = 0.95
P(
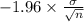 <
<
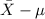 <
<
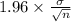 ) = 0.95
) = 0.95
P(
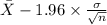 <
<
 <
<
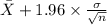 ) = 0.95
) = 0.95
95% confidence interval for
 = [
= [
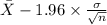 ,
,
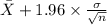 ]
]
= [
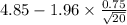 ,
,
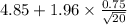 ]
]
= [4.52 , 5.18]
Therefore, 95% confidence interval for the true average porosity of a certain seam is [4.52 , 5.18].
(b) Now, there is another seam based on 16 specimens with a sample average porosity of 4.56.
The pivotal quantity for 98% confidence interval for the population mean is given by;
P.Q. =
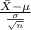 ~ N(0,1)
~ N(0,1)
where,
 = sample average porosity = 4.56
= sample average porosity = 4.56
 = population standard deviation = 0.75
= population standard deviation = 0.75
n = sample of specimens = 16
 = true average porosity
= true average porosity
Here for constructing 98% confidence interval we have used One-sample z test statistics as we know about population standard deviation.
So, 98% confidence interval for the true mean,
 is ;
is ;
P(-2.3263 < N(0,1) < 2.3263) = 0.98 {As the critical value of z at 1% level
of significance are -2.3263 & 2.3263}
P(-2.3263 <
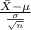 < 2.3263) = 0.98
< 2.3263) = 0.98
P(
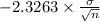 <
<
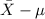 <
<
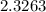 ) = 0.98
) = 0.98
P(
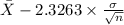 <
<
 <
<
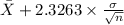 ) = 0.98
) = 0.98
98% confidence interval for
 = [
= [
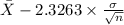 ,
,
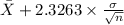 ]
]
= [
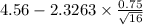 ,
,
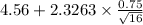 ]
]
= [4.12 , 4.99]
Therefore, 98% confidence interval for the true average porosity of a another seam is [4.12 , 4.99].