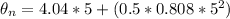Answer:
a
The angular acceleration is
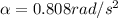
b
The average angular velocity is
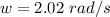
c
The instantaneous angular velocity is
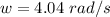
d
The additional angle (rad) will the disk turn during the next 5.00 s is

Step-by-step explanation:
From the question we are told that
The duration of rotation is
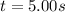
The angular displacement is
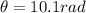
From newtons Law the angular displacement is mathematically represented as
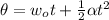
Where
 is the angular acceleration
is the angular acceleration
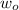 is the initial angular velocity and its value is 0
is the initial angular velocity and its value is 0
Making
 the subject of formula
the subject of formula
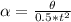
Substituting value
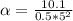
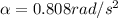
The average angular velocity is mathematically represented as
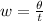
Substituting value
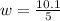
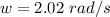
From the equations of motion the instantaneous angular velocity is mathematically represented as

Substituting value
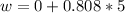
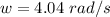
Modifying the equation for angular displacement is mathematically represented as
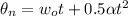
From the question
 is not changed
is not changed
t = 5s
the initial velocity would be the instantaneous velocity
So
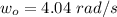
Substituting value