Question

A lot of 25 skylight covers are received at your construction site, and before installation are subjected to an acceptance testing procedure. The procedure consists of selecting 5 covers at random, without replacement, and testing each one using projectile to simulate hail stone impacts. If 2 or fewer of the 5 covers crack, the remaining ones are accepted. Otherwise the lot is rejected and sent back to the supplier. Assume a lot actually has four defective covers (impact strength is not adequate to withstand the test) among the 25. What is the exact probability of lot acceptance? Hint: Hypergeometric.

Answer 1

If the lot has 4 defective covers out of 25 total covers, the probability of accepting the lot is P=0.98.

Explanation:

We have a population of N=25 skylight covers, were K=4 are defective.

We sample n=5 covers, and we will accept the lot if k=2 or fewer are defective.

We will use the hypergeometric distribution to model this probabilities.

First, to be accepted, the sample can have 2, 1 or 0 defective covers, so the probability of being accepted is:

`P(accepted)=P(k\leq2)=P(k=0)+P(k=1)+P(k=2)`

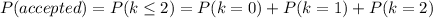
The probability that there are k defective covers in the sample is:

`P(k)=\frac{\dbinom{k}{k}\dbinom{N-k}{n-k}}{\dbinom{N}{n}}`

Then, we can calculate the individual probabilities as:

`P(k=0)=\frac{\dbinom{4}{0}\cdot \dbinom{25-4}{5-0}}{\dbinom{25}{5}}=\frac{\dbinom{4}{0}\cdot \dbinom{21}{5}}{\dbinom{25}{5}}\\\\\\P(k=0)=(1\cdot 20349)/(53130)=0.38`

`P(k=1)=\frac{\dbinom{4}{1}\cdot \dbinom{25-4}{5-1}}{\dbinom{25}{5}}=\frac{\dbinom{4}{1}\cdot \dbinom{21}{4}}{\dbinom{25}{5}}\\\\\\P(k=1)=(4\cdot 5985)/(53130)=0.45`

`P(k=2)=\frac{\dbinom{4}{2}\cdot \dbinom{25-4}{5-2}}{\dbinom{25}{5}}=\frac{\dbinom{4}{2}\cdot \dbinom{21}{3}}{\dbinom{25}{5}}\\\\\\P(k=2)=(6\cdot 1330)/(53130)=0.15`

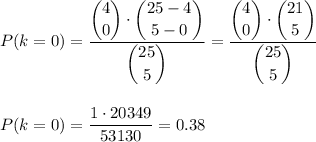
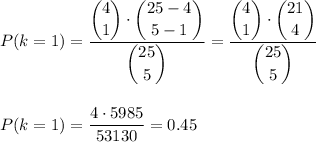
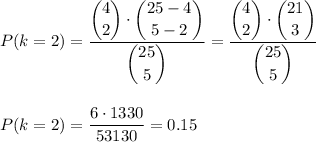
If we add this probabilities, we have:

`P(accepted)=P(k\leq2)=P(k=0)+P(k=1)+P(k=2)\\\\P(accepted)=0.38+0.45+0.15=0.98`

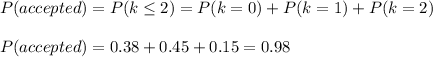
If the lot has 4 defective covers out of 25 total covers, the probability of accepting the lot is P=0.98.