Question

Suppose that all the people in a country are ranked according to their​ incomes, starting at the bottom. Let x represent the fraction of the community making the lowest income (0 less than or equals x less than or equals 1 )​; x equals 0.4​, ​therefore, represents the lower​ 40% of all income producers. Let​ I(x) represent the proportion of the total income earned by the lowest x of all people.​ Thus, I(0.4) represents the fraction of total income earned by the lowest​ 40% of the population. The curve described by this function is known as a Lorenz curve. Suppose Upper I (x )equals 0.94 x squared plus 0.06 x. Find and interpret (0.1).

Answer 1

I(0.1) = 0.0154

The 10% of the community with the lowest income hold 1.54% of the total income earned in the community.

Explanation:

The Lorenz curve is given by:

`I(x) = 0.94x^2+0.06x`

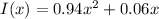
If x = 0.1 (representing the 10% of the community with the lowest income), their total aggregate income is given by:

`I(x) = 0.94*0.1^2+0.06*0.1\\I(x) = 0.0154=1.54\%`

This means that the 10% of the community with the lowest income hold 1.54% of the total income earned in the community.