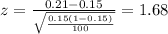Question

A quality control engineer at a potato chip company tests the bag filling machine by weighing bags of potato chips. Not every bag contains exactly the same weight. But if more than 15% of bags are over-filled then they stop production to fix the machine. They define over-filled to be more than 1 ounce above the weight on the package. The engineer weighs 100 bags and finds that 21 of them are over-filled. He plans to test the hypotheses H 0: p = 0.15 versus H a : p > 0.15. What is the test statistic?

Answer 1

`z=\frac{0.21 -0.15}{\sqrt{(0.15(1-0.15))/(100)}}=1.68`

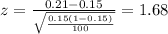
Explanation:

Information provided

n=100 represent the random sample taken

X=21 represent the number of bags overfilled

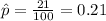`\hat p=(21)/(100)=0.21` estimated proportion of overfilled bags

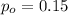`p_o=0.15` is the value that we want to test

z would represent the statistic

Hypothesis

We need to conduct a hypothesis in order to test if the true proportion of overfilled bags is higher than 0.15.:

Null hypothesis:
`p =0.7`

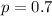
Alternative hypothesis:
`p > 0.15`

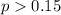
The statistic for this case is:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

And replacing the info given we got:

`z=\frac{0.21 -0.15}{\sqrt{(0.15(1-0.15))/(100)}}=1.68`