Answer:
The correct option is (A).
Explanation:
The multiple linear regression equation is given by,
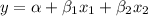 , where α = constant and β
, where α = constant and β
 = slope coefficients of regression line.
= slope coefficients of regression line.
To test if there is a important relationship amid X
 and Y, we use the t-statistic test.
and Y, we use the t-statistic test.
The t-statistic for regression coefficient analysis is given by,
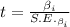
The regression equation for test scores dependent upon the two explanatory variables, the student-teacher ratio and the percent of English learners is:
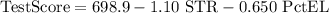
A t-test for the significance of the regression coefficient of variable student-teacher ratio (STR) is conducted.
The test statistic is found to be, t = 2.56.
The regression coefficient of variable STR is, 1.10.
Compute the standard error of the regression coefficient as follows:
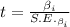


The standard error of the regression coefficient is 0.43.
Thus, the correct option is (A).