Answer:
a)

b)

c) Assuming a the normality assumption we will have within 2 deviations from the mean most of the data from the distribution and the interval for this case would be:

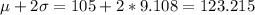
So we expect about 86 and 123 most of the numbers of Caesarian section births
Explanation:
For this case we can define the random variable X as the number of births in the Caesarian section and from the data given we know that the distribution of X is:
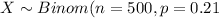
Part a
The expected value for this distribution is given by:

Part b
The variance is given by:
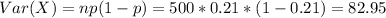
And the deviation would be:

Part c
Assuming a the normality assumption we will have within 2 deviations from the mean most of the data from the distribution and the interval for this case would be:

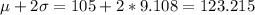
So we expect about 86 and 123 most of the numbers of Caesarian section births