Answer:
a)
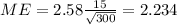
b)
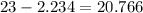
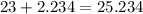
c) We are 99% confident that the true mean for the costs of an order for the local pizzeria is between 20.766 and 25.234
d) For this case if we decrease the confidence then the margin of error would be lower and that implies a narrower interval. Becuase the critical value is lower if the decrease the confidence level
Explanation:
Data provided
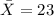 represent the sample mean for the cost of orders
represent the sample mean for the cost of orders
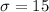 represent the sample population deviation
represent the sample population deviation
n=300 represent the sample size
Part a
The confidence interval for a true mean is given by:
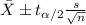 (1)
(1)
And the margin of error is given by:
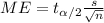
The Confidence is 0.99 or 99%, the significance is
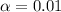 and
and
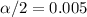 , and the critical value would be
, and the critical value would be

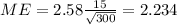
Part b
The confidence interval would be:
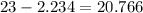
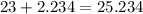
Part c
We are 99% confident that the true mean for the costs of an order for the local pizzeria is between 20.766 and 25.234
Part d
For this case if we decrease the confidence then the margin of error would be lower and that implies a narrower interval. Becuase the critical value is lower if the decrease the confidence level