Answer:
perimeter=28.85 cm
Explanation:
Hello, I can help you with this
in this case, in this case it is posible divide the area into 2 more known shapes, a rectangle and a semicircle
let's remember
the area of a rectangle is given by
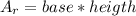
the area of a semicircle is given by

so, the total area is

Step one
Let
base=5 cm
heigth=8 cm
diameter of the circle=5 cm
Step 2
put the values into the equation

so, the total area is 49.81215 square centimeters
to find the perimeter you must add the sides of the rectangle
it is
perimeter of the rectangle =8+8+5=21 cm
now, the perimeter of the semicircle is =pi* radius
Perimeter=(3.14*diameter)/2
Perimeter=(3.14*5)/2
Perimeter=7.85
so, the total perimeter is =21 cm+7.85
total perimeter=28.85
Have a good day.