Question

A study of immunizations among school‑age children in California found that some areas had rates of unvaccinated school‑age children as high as 13.5%13.5% in 2014. Imagine a classroom of 2020 children in one such area where 13.5%13.5% of children are unvaccinated. If there are no siblings in the classroom, we are willing to consider the vaccination status of the 2020 unrelated children to be independent. (a) Obtain the probability that none of the 2020 children in such a classroom would be unvaccinated. (Enter your answer rounded to three decimal places.)

Answer 1

Probability that none of the 20 children in such a classroom would be unvaccinated is 0.055.

Explanation:

We are given that a classroom of 20 children in one such area where 13.5% of children are unvaccinated.

If there are no siblings in the classroom, we are willing to consider the vaccination status of the 2020 unrelated children to be independent.

The above situation can be represented through binomial distribution;

`P(X=r) = \binom{n}{r} * p^(r) * (1-p)^(n-r) ; x = 0,1,2,3,......`

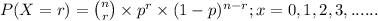
where, n = number of trials (samples) taken = 20 children

r = number of success = none of the 20 children

p = probability of success which in our case is probability that

children are unvaccinated, i.e; p = 13.5%

Let X = Number of children that are unvaccinated

So, X ~ Binom(n = 20, p = 0.135)

Now, Probability that none of the 20 children in such a classroom would be unvaccinated is given by = P(X = 0)

P(X = 0) =
`\binom{20}{0} * 0.135^(0) * (1-0.135)^(20-0)`

=
`1* 1 * 0.865^(20)`

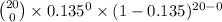
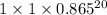
= 0.055

Hence, the probability that none of the 20 children in such a classroom would be unvaccinated is 0.055.