Question

Renowned French chef Pierre Blaireau is planning a five-course meal for his restaurant’s guests. His different choices include 10 light appetizers, 12 salads, 5 small risotto-based entr´ees, 7 seafood-based dishes and 5 desserts (all those categories are exclusive; there is no dish that, e.g, is both an entr´ee and a dessert). Chef Blaireau inspects his ingredients for quality and freshness and throws away 3 salads and 2 kinds of seafood. How many five-course meals can he make after this?

Answer 1

He can make 11,250 five-course meals after this

Explanation:

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

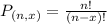
In this problem:

The options are:

10 light appetizers

12 salads

5 small entrees

7 dishes

5 desserts

He throws away

3 salads

2 kinds of dishes

So he will choose

One light appetizer, from a set of 10

One salad, from a set of 9

One entree, from a set of 5

One dish, from a set of 5

One dessret, from a set of 5.

So

`T = P_((10,1)) * P_((9,1)) * P_((5,1)) * P_((5,1)) * P_((5,1)) = (10!)/((10-1)!) * (9!)/((9-1)!) * (5!)/((5-1)!) * (5!)/((5-1)!) * (5!)/((5-1)!) = 11250`

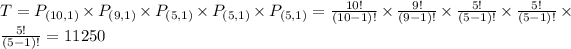
He can make 11,250 five-course meals after this