Question

An inductor is connected to a voltage source and it is found that it has a time constant, t. When a 10-ohm resistor is placed in series with the inductor, the time constant becomes t/2. A pure inductance of 30 mH is placed in series with the original inductor and the 10-ohm resistor, the time constant is t. What are the values of the original inductors (a) inductance, (b) internal resistance

Answer 1

A) 30 mH

B ) 10-ohm

Step-by-step explanation:

resistor = 10-ohm

Inductor = 30mH ( l )

L = inductance

R = resistance

r = internal resistance

values of the original Inductors

Note : inductor = constant time (t) case 1

inductor + 10-ohm resistor connected in series = constant time ( t/2) case2

inductor + 10-ohm resistor + 30 mH inductance in series = constant time (t) case3

From the above cases

case 1 = time constant ( t ) = L / R

case 2 = Req = R + r hence time constant t / 2 = L / R + r therefore

t =
`(2L)/(R+r)`

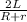
case 3 = Leq = L + l , Req = R + r . constant time ( t )

hence Z =
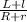`(L + l)/(R + r)` = t

A) Inductance

To calculate inductance equate case 1 to case 3

`(L)/(R)` =
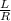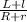`(L + l)/(R + r)` = L / 10 = (L + 30) / ( 10 + 10 )

= 20 L = 10 L + 300 mH

10L = 300 m H

therefore L = 30 mH

B ) The internal resistance

equate case 1 to case 2

`(L)/(R)` =
`(2L)/(R + r)`

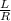R + r = 2 R therefore ( r = R ) therefore internal resistance = 10-ohm