Question

Two long, parallel, current-carrying wires lie in an xy-plane. The first wire lies on the line y = 0.320 m and carries a current of 30.0 A in the +x direction. The second wire lies along the x-axis. The wires exert attractive forces on each other, and the force per unit length on each wire is 290 µN/m. What is the y-value (in m) of the line in the xy-plane where the total magnetic field is zero?

Answer 1

y = 0.108m

Step-by-step explanation:

The magnitude of the magnetic force is given by:

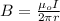`B=(\mu_oI)/(2\pi r)` ( 1 )

and the force per unit length is:

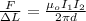`(F)/(\Delta L)=(\mu_oI_1I_2)/(2\pi d)` ( 2 )

you first calculate I2 from (2):

`I_2=((F)/(\Delta L))(2\pi d)/(\mu_o I_1)=(290*10^(-6)N/m)(2\pi (0.320m))/((4\pi*10^(-7)m)(30.0A))=15.46A`

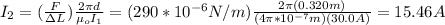
With this values of I2 you can the position in which the magnitude of the magnetic field is zero, by using (1) for both wires:

`(\mu_o)/(2\pi)[(I_1)/(0.320-r)-(I_2)/(r)]=0\\\\I_1r=I_2(0.320-r)\\\\r(I_1+I_2)=0.320I_2\\\\r=(0.320I_2)/(I_1+I_2)=(0.320(15.46))/(15.46+30.0)=0.108m`

hence, for y=0.108m the magnitude of B is zero