Answer:
The equilibrium constant is
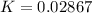
The equilibrium pressure for oxygen gas is

Step-by-step explanation:
From the question we are told that
The equation of the chemical reaction is
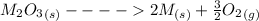
The Gibbs free energy for
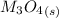 is
is
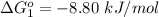
The Gibbs free energy for
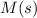 is
is

The Gibbs free energy for
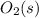 is
is
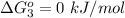
The Gibbs free energy of the reaction is mathematically represented as
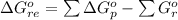
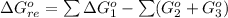
Substituting values
From the balanced equation
![\Delta G^o_(re) =[ (2 * 0) + ((3)/(2) * 0 )] - [1 * - 8.80]](https://img.qammunity.org/2021/formulas/chemistry/college/e1s081d8njoh1ir4nmw68vvsuvi17as9ua.png)
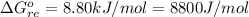
The Gibbs free energy of the reaction can also be represented mathematically as

Where R is the gas constant with a value of
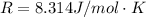
T is the temperature with a given value of
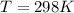
K is the equilibrium constant
Now equilibrium constant for a reaction that contain gas is usually expressed in term of the partial pressure of the reactant and products that a gaseous in state
The equilibrium constant for this chemical reaction is mathematically represented as
![K_p =[ P_(O_2)]^{(3)/(2) }](https://img.qammunity.org/2021/formulas/chemistry/college/2zptxunhuol5scc1yuul3frr1b1r0iwenm.png)
Where
![[ P_(O_2)]](https://img.qammunity.org/2021/formulas/chemistry/college/4gpwlocicqn83w8l6h3p36gyrnhv5uu3vr.png) is the equilibrium pressure of oxygen
is the equilibrium pressure of oxygen
The p subscript shows that we are obtaining the equilibrium constant using the partial pressure of gas in the reaction
Now equilibrium constant the subject on the second equation of the Gibbs free energy of the reaction

Substituting values
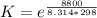
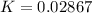
Now substituting this into the equation above to obtain the equilibrium of oxygen
![0.02867 = [P_(O_2)]^{[(3)/(2) ]}](https://img.qammunity.org/2021/formulas/chemistry/college/wg1s9gd2blb4kwvd39spba34680mr6tfc2.png)
multiplying through by

![P_(O_2) = [0.02867]^{(2)/(3) }](https://img.qammunity.org/2021/formulas/chemistry/college/pdyxxnhd6w636i8dwzqbnpr1hpz5l2v9nh.png)
