Question

Describe the graph of the function.

y = 2x2 + 12x – 15


The graph is a parabola with axis of symmetry at x = –3.


The graph is a parabola with axis of symmetry at x = 3.


The graph is a parabola with axis of symmetry at x = 15.


The graph is a parabola with axis of symmetry at x = 2.

Answer 1

B

Explanation:

EDGE2020

Answer 2

The answer is option 1.

Explanation:

Axis of symmetry means the middle x-coordinates of the parabola. So in order to find the x value, you have to find the TP which is Turning Point by using Completing the Square :

`{(x + (b)/(2) )}^(2) - {( (b)/(2) )}^(2) + c = 0`

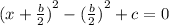
Let y = 0,

`2{x}^(2) + 12x - 15 = 0`

`2( {x}^(2) + 6x - (15)/(2) ) = 0`

`{( {x + (6)/(2)) }^(2) - ( { (6)/(2) )}^(2) - (15)/(2) } = 0`

`( {x + 3)}^(2) - {(3)}^(2) - (15)/(2) = 0`

`( {x + 3)}^(2) - 9 - (15)/(2) = 0`

`(x { + 3)}^(2) - (33)/(2) = 0`

`2(x { + 3)}^(2) - 33 = 0`

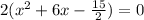
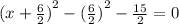
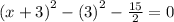
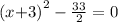
Next, you have to solve the x value :

x + 3 = 0

x = -3